Lattice theorem
In mathematics, the lattice theorem, sometimes referred to as the fourth isomorphism theorem or the correspondence theorem, states that if  is a normal subgroup of a group
is a normal subgroup of a group  , then there exists a bijection from the set of all subgroups
, then there exists a bijection from the set of all subgroups  of
of  such that
such that  contains
contains  , onto the set of all subgroups of the quotient group
, onto the set of all subgroups of the quotient group 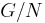 . The structure of the subgroups of
. The structure of the subgroups of 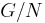 is exactly the same as the structure of the subgroups of
is exactly the same as the structure of the subgroups of  containing
containing 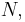 with
with  collapsed to the identity element.
collapsed to the identity element.
This establishes a monotone Galois connection between the lattice of subgroups of  and the lattice of subgroups of
and the lattice of subgroups of 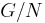 , where the associated closure operator on subgroups of
, where the associated closure operator on subgroups of  is
is 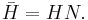
Specifically, If
- G is a group,
- N is a normal subgroup of G,
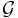 is the set of all subgroups A of G such that
is the set of all subgroups A of G such that 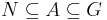 , and
, and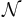 is the set of all subgroups of G/N,
is the set of all subgroups of G/N,
then there is a bijective map 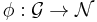 such that
such that
 for all
for all 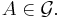
One further has that if A and B are in 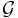 , and A' = A/N and B' = B/N, then
, and A' = A/N and B' = B/N, then
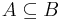 if and only if
if and only if 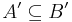 ;
;- if
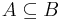 then
then 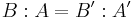 , where B:A is the index of A in B (the number of cosets bA of A in B);
, where B:A is the index of A in B (the number of cosets bA of A in B); 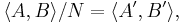 where
where 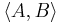 is the subgroup of
is the subgroup of  generated by
generated by 
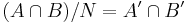 , and
, and is a normal subgroup of
is a normal subgroup of  if and only if
if and only if 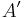 is a normal subgroup of
is a normal subgroup of 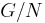 .
.
This list is far from exhaustive. In fact, most properties of subgroups are preserved in their images under the bijection onto subgroups of a quotient group.
See also
References
- W.R. Scott: Group Theory, Prentice Hall, 1964.